ACTF2020密码学部分writeup

编写的项目文件请参考项目链接。同时欢迎大家访问ACTF2020的所有赛题。喜欢的话请多多资瓷一下，给我们实验室的项目加个Star或者Fork，谢谢。

为了保护服务器的同时不给选手带来更多困难，密码学部分的交互题开了pow算力检测，我也提供了相应的pow算力运算解决样例，大家下载即可。

入门题

Column Permutation Cipher：

简单的矩阵换位密码，首先统计字段长度为625，由于题目中告诉我们是m*n矩阵换位，所以m,n的可能值是(5,125),(25,25),(125,5)，然后爆破即可，示例脚本:

#-*- coding=UTF-8 -*-
possiblelen=[5,25,125]
for k in possiblelen:
    plaintext=""
    line=625//k
    for i in range(k):
        for j in range(line):
            plaintext+=cipher[j*k+i]
    print(plaintext)

我的密码本:

统计英文文本中每个字符的出现频率，并查找概率表进行对比。当然其中需要用到一些英文知识，一般这种题目语义都是连贯的，一定要注意最后解出来的明文语义上是否通顺。

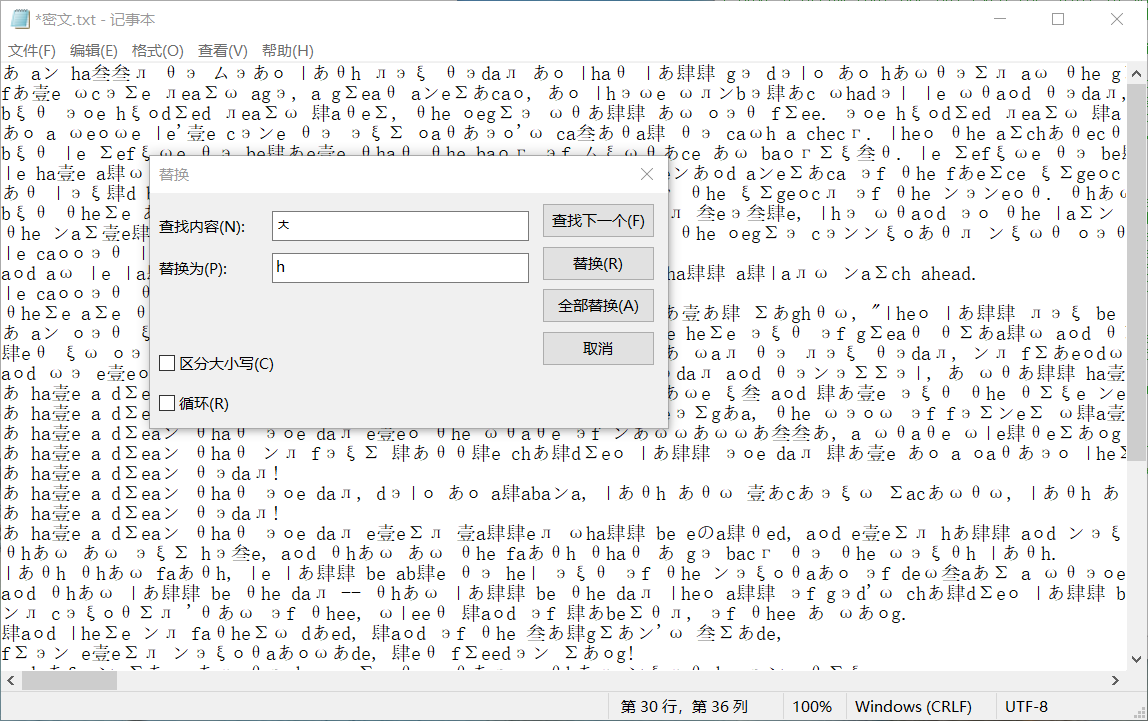
如果你统计好词频并确定了明文-密文对以后，即可还原出原文。

code_book="ㅡ贰ㅒㄱёㄴ伍ㅊあムг肆ンㅇэ叁йΣωθξ壹ㅣのл￥"
plaintext=""
for j in range(len(cipher)):
    flag=0
    for i in range(len(code_book)):
        if(cipher[j]==code_book[i]):
            plaintext+=str(chr(0x61+i))
            flag=1
    if(flag==0):
        plaintext+=cipher[j]
print(plaintext)

简单题

bomb or boom：

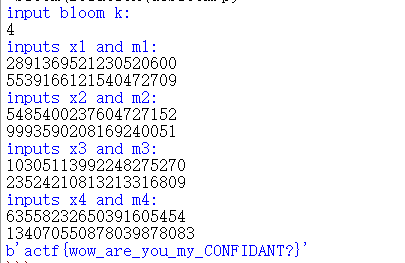
题目给出了5个压缩包文件和一个密码本，并告知我们5个压缩包只要破解4个就行。所以应该涉及到门限方案，这里虽然没有题目名，但是hint中给出来了，用的是bloom门限。这是一个（4,5）门限，消息被5个随机模数求模，得到a_i和m_i。并被封装在五个压缩包中。

压缩包的密码被一些编码方式加密了，想了解这些编码方式请看这里。

下面稍微解释一下这些有趣的编码，第一个是培根，第二个盲文，第三个用的是千千秀字的文本转音符（大可搜索一下，如何把文本加密为音符，仅此一家，ps.看着音符的样子难道不好看嘛），第四个是aaencode（学过web应该都知道的吧），第五个是brainfuck，参考一下资料即可。

然后用门限方案的脚本直接跑，就可以辽：

import math
from Cryptodome.Util.number import *
import gmpy2
def re(w1,m1):#乘法逆
	t1=w1
	t2=m1
	i=0
	s=[]
	while(t1):
		y=t2%t1
		s.append(int(t2//t1))
		t2=t1
		t1=y
	re1= 0
	re2= 1
	i=len(s)-2	
	while(i>=0):
		t=re2
		re2=re1*1-re2*s[i]
		re1=t
		i-=1
	return re2
def debloom(k):
    x=[]
    m=[]
    for i in range(0,k):
        print("inputs x"+str(i+1)+" and m"+str(i+1)+":")
        x.append(int(input()))
        m.append(int(input()))
    Mn=1
    for i in range(0,k):
        Mn=Mn*m[i]

    w=[]
    for i in range(0,k):
        w.append(int(Mn//m[i]))
    t=[]
    for i in range(0,k):
        t.append(re(w[i],m[i]))
    result=0#初始化
    for i in range(0,k):
        result+=(w[i]*t[i]*x[i])
    result=result%Mn
    print(long_to_bytes(result))

print("input bloom k:")
k=int(input())
debloom(k)

运行结果：

naive encryption:

一道改装后的仿射密码题，只不过采用了不同的a,b进行了更多的轮加密，所以说这道题目更像是算法逆向。关键知识是乘法逆。解题脚本如下：

from Cryptodome.Util.number import *

def inv(u,v):
    u3,v3=u,v
    u1,v1=1,0
    while v3>0:
        q=u3//v3
        u1,v1=v1,u1-v1*q
        u3,v3=v3,u3-v3*q
    while u1<0:
        u1=u1+v
    return u1
    

k=[3,5,7,11,13,17,19,23,29,31,37,
    41,43,47,53,59,61,67,71,73,79,
    83,89,97,101,103,107,109,113,
    127,131,137,139,149,151,157,
    163,167,173,179,181,191,193,
    197,199,211,223,227,229,233,
    239,241,251]
n=1000
len_k=len(k)
cipher=[71, 37, 4, 242, 109, 227, 22, 207, 36, 5, 39, 87, 22, 155, 19, 5, 19, 36, 155, 36, 224, 2, 104, 155, 39, 2, 19, 241, 155, 70, 210, 241, 53, 5, 19, 39, 22, 70, 22, 210, 70, 75]

flag=0
len_cipher=len(cipher)
while(n>0):
    pointer=1001-n
    for i in range(len_cipher):
        #cipher[i]=(cipher[i]*k[((pointer+2)%len_k]+k[(pointer*7)%len_k])&0xff
        cipher[i]=((cipher[i]-k[(pointer*7)%len_k])*inv(k[(pointer+2)%len_k],0x100))&0xff
    n=n-1
for i in range(0,len_cipher):
    flag+=cipher[i]
    flag=flag<<8
flag=flag>>8
print(long_to_bytes(flag))

naive rsa：

本来这道题目我已经出好推送想送分的，但不料推送还没轮到我，所以没发出来，希望大家多多支持“中南极光网安实验室”的公众号，支持痛并快乐着的作品。

回到题目，这是一道简单的coppersmith，主要问题出在getPrime函数和给出的p%q上。p是520位素数，q是500位素数，所以p//q就在2¹⁹到2²¹之间，我们假设p//q=k，p%q=a，那么p=kq+a，那么我们只需要在2¹⁹到2²¹之间爆破k即可，脚本如下：

import gmpy2
from Cryptodome.Util.number import *
a=int(input())
N=int(input())
c=int(input())
e=65537
for k in range(2**19,2**21):
    #print(gmpy2.iroot(k*k+4*N, 2)[0])
    q = (-a + gmpy2.iroot(a*a+4*k*N, 2)[0])//(2*k)
    p = k*q+a
    #print(k)
    if(p*q==N):
        #print (k)
        phi = (p-1)*(q-1)
        d = gmpy2.invert(e,phi)
        m = pow(c,d,N)
        print (long_to_bytes(m))
        break

中等题

Imitation game：

由于在密码学实验期间，我发现基本没有同学完成mtp的实验，所以在这里稍微加深了一下mtp以后形成了新的题目。这道题目和一般的mtp的区别就是，这里对密钥进行了类似于CBC的块加密，代码如下：

def encrypt(iv,message):
    padding=[iv]   
    cipher=[message[0]^padding[0]]
    for i in range(1,len_flag):
        #print(cipher)
        padding.append(cipher[i-1]^padding[i-1])
        cipher.append(message[i]^padding[i])
    print("cipher={}".format(cipher))

但是由于初始iv范围很小，而且它嵌入到了密钥的每一个字节中，所以我们只需要爆破iv就可以得到明文。甚至我们可以知道密钥最后一位是”}”，直接与mtp后得到的密钥异或就知道iv值了。然后整个密钥每个字节异或iv就得到明文。

而对于mtp，题目中已经给出，密文都来自于书本原句，即可见字符，那么我们只需要通过限定课件字符的范围就可以排除很多无关答案。这里推荐python的mtp包，效果很棒，运行截图如下：

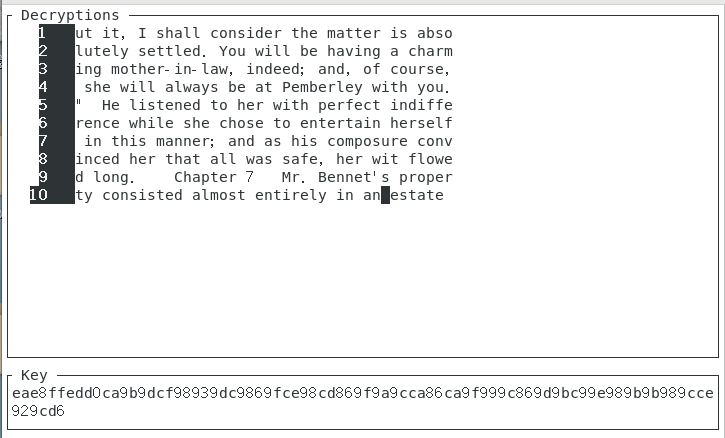
得到的key不是最后的key，但是0xd6^b’}’=0xab，所以对每一位异或0xab即可得到明文。

naive aes：

又是一道算法逆向题，但是这里主要考察的是S盒和P盒的逆向。

from： nactf——Super Duper AES

writeup: detail link

all you need is to:

1.Reverse the permute() function.

2.Reverse the substitute() function.

3.Put everything together and run the script.

Isn’t it easy?

tiny_PRNG0:

出题人：DJ

出题人只给了我脚本，不过mt19937伪随机数预测最近的CTF题目很多，大家可以参考这个博客。

基本思想：根据输出的随机数逆向extract_number对应的状态，实际上只需要前624个随机数恢复前624个state，就可以预测此后生成的随机数。 脚本：

1.mt19937.py

#!/usr/bin/env python3
# -*- coding: utf-8 -*-

def inv_right_shift(v, b, m):
    '
        >>> from cryptonita.attacks.prng import inv_right_shift
        >>> y, b, m = 524889969, 11, 0x010101
        >>> v = y ^ ((y >> b) & m)
        >>> inv_right_shift(v, b, m)
        524889969
        >>> y, b, m = 0xffffffff, 4, 0xffffffff
        >>> v = y ^ ((y >> b) & m)
        >>> inv_right_shift(v, b, m)
        4294967295
    '
    assert 0 < b < 32

    g = 0
    i = 0
    while i < 32:
        g = v ^ ((g >> b) & m)
        i += b

    return g

def inv_left_shift(v, b, m):
    '
        >>> from cryptonita.attacks.prng import inv_left_shift
        >>> y, b, m = 524889969, 3, 0x010101
        >>> v = y ^ ((y << b) & m)
        >>> inv_left_shift(v, b, m)
        524889969
        >>> y, b, m = 0xffffffff, 4, 0xffffffff
        >>> v = y ^ ((y << b) & m)
        >>> inv_left_shift(v, b, m)
        4294967295
    '
    assert 0 < b < 32

    g = 0
    i = 0
    while i < 32:
        g = v ^ ((g << b) & m)
        i += b

    return g

def clone_mt19937(out):
    '   Clone the internal state of a Mersenne Twister 19937 (MT19937)
        from its output <out>.
        For MT19937 we need 624 sequential bytes at minimum to clone
        the state.
            >>> from cryptonita.attacks.prng import clone_mt19937
            >>> clone_mt19937(B('abc'))           # byexample: +norm-ws
            Traceback <...>
            ValueError: You need at least 624 bytes to clone the MT19937 PRNG
                        but you have only 3.
        With 624+n, the first 624 are used to clone the
        MT19937's state and the next byte is used to validate.
        If the validation fails, "shift to the right one byte": the first
        byte is ignored, the next 624 bytes are used to re-clone the state
        and the next byte is used to validate the generator.
        The process continues until one validation success or until reach the
        end of the string.
        The last cloned MT19937 cannot be validated.
        Given 624 bytes only, no validation is performed; given 624*2 bytes,
        it is guaranteed that a valid clone can be found.
        '

    n = 624
    if len(out) < n:
        raise ValueError(("You need at least %i bytes to clone the MT19937 PRNG" +\
                          " but you have only %i.") % (n, len(out)))

    u, d = 11, 0xffffffff
    s, b = 7, 0x9d2c5680
    t, c = 15, 0xefc60000
    l = 18

    state = []
    for y in out:
        y = inv_right_shift(y, l, 0xffffffff)    # inv of y ^ ((y >> l) & 0)
        y = inv_left_shift(y, t, c)     # inv of y ^ ((y << t) & c)
        y = inv_left_shift(y, s, b)     # inv of y ^ ((y << s) & b)
        y = inv_right_shift(y, u, d)    # inv of y ^ ((y >> u) & d)

        state.append(y)

    found = False
    i = 0
    g = MT19937(0)
    g.reset_state(state[i:i+n], index=n)

    while i+n < len(out):
        v = g.extract_number()
        found = v == out[i+n]
        if found:
            g.reset_state(state[i:i+n], index=n)
            break

        i += 1
        g.reset_state(state[i:i+n], index=n)

    return g

# https://en.wikipedia.org/wiki/Mersenne_Twister
class MT19937:
    def __init__(self, seed):
        w, n, m, r = 32, 624, 397, 31
        a, f = 0x9908b0df, 1812433253
        W = 0xffffffff
        u, d = 11, 0xffffffff
        s, b = 7, 0x9d2c5680
        t, c = 15, 0xefc60000
        l = 18

        # Create a length n array to store the state of the generator
        self.MT = MT = [] # n size
        self.index = n+1
        lower_mask = (1 << r) - 1
        upper_mask = (~lower_mask) & W

        # Initialize the generator from a seed
        index = n
        MT.append(seed)
        for i in range(1, n):
            MT.append((f * (MT[i-1] ^ (MT[i-1] >> (w-2))) + i) & W)


        # Generate the next n values from the series x_i
        def twist():
            for i in range(n):
                 x = (MT[i] & upper_mask) \
                           + (MT[(i+1) % n] & lower_mask)

                 xA = x >> 1
                 if (x % 2) != 0:  # lowest bit of x is 1
                     xA = xA ^ a

                 MT[i] = MT[(i + m) % n] ^ xA

            self.index = 0

        # Extract a tempered value based on MT[index]
        # calling twist() every n numbers
        def extract_number():
            while 1:
                if self.index >= n:
                    twist()

                y = MT[self.index]
                y = y ^ ((y >> u) & d)
                y = y ^ ((y << s) & b)
                y = y ^ ((y << t) & c)
                y = y ^ (y >> l)

                self.index += 1
                yield y & W

        self.extract_number = extract_number

    def reset_state(self, MT, index=0):
        assert len(MT) == len(self.MT)

        self.index = index
        if not (0 <= self.index <= len(MT)):
            raise IndexError("Setting index=%i is out of range" \
                    % (self.index))

        self.MT[:] = MT

    def __iter__(self):
        return self.extract_number()

2.exp.py

#!/usr/bin/env python3
# -*- coding: utf-8 -*-

from sys import argv
from typing import List
from tqdm import tqdm
from mt19937 import clone_mt19937
import re 
from pwn import (
    process,
    remote,
    log,
    # context
)
# context.log_level = "DEBUG"


def get_output(io, size):
    output = []
    with tqdm(total=size) as bar:
        while len(output) < size:
            io.sendlineafter("> ", "1")
            line = io.recvline().decode("utf-8")
            output += list(map(int, line.strip().split(" ")))
            bar.update(10)
    bar.close()
    return output

def main():
    if len(argv) == 1:
        io = process("./a.out")
    else:
        io = remote(argv[1], int(argv[2]))
    log.info("get output from mt19937")
    out = get_output(io, 640)
    log.info("clone mt19937 from output")
    new_iter = iter(clone_mt19937(out))
    io.sendline("2")
    log.info("send answer")
    io.sendline(str(next(new_iter)))
    s = str(io.recvuntil("4) "))
    s = str(io.recvuntil("4) "))
    log.success(re.search("ACTF{.*}", s).group(0))

if __name__ == "__main__":
    main()

难题

DLP头号玩家：

这道题主要是想考察离散对数问题，设计的考点有：如何计算离散对数，ElGamal算法，ecc算法。

level1:计算离散对数

采用大步小步法即可。

level2：ElGamal算法

首先，这里的密钥是两个字节的（见下面代码），可以直接考虑爆破：

d=bytes_to_long(message[0:2])

然后根据密钥进行ElGamal算法解密即可。

level3：ECC算法

先回顾一下ECC算法

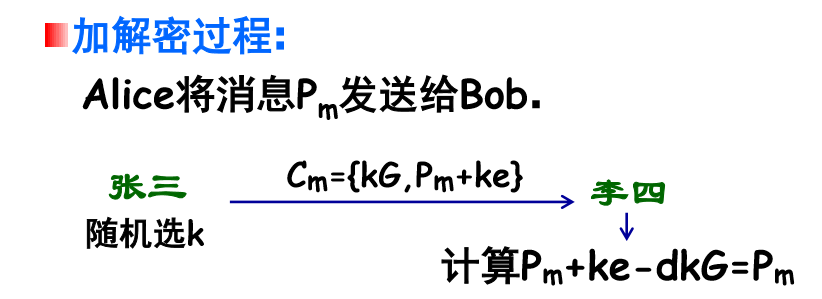
这里我在具体代码中做了一些手脚，令k=100,d=100，把100当成常量嵌入到了kG的运算中，所以其实解密的时候只需要代入d=100,k=100即可。

解题脚本示例如下(省略交互)：

from math import ceil,sqrt
from Cryptodome.Util.number import *
from ecc import get_inverse,get_gcd,get_np,get_ng
def bsgs(g, y, p):
    res = []
    m = int(ceil(sqrt(p - 1)))
    S = {pow(g, j, p):j for j in range(m)}
    gs = pow(g, p - 1 - m, p)
    for i in range(m):
        if y in S:
            res.append(i * m + S[y])
        y = y * gs % p
    return res

def get_inverse(u,v):
    u3,v3=u,v
    u1,v1=1,0
    while v3>0:
        q=u3//v3
        u1,v1=v1,u1-v1*q
        u3,v3=v3,u3-v3*q
    while u1<0:
        u1=u1+v
    return u1

#level1
p=5391644857
g=2
c1=[4908063849,1283736637,4385640372,428852363]
for i in range(len(c1)):
    inp=c1[i]
    c=int(inp)
    res=bsgs(g,c,p)
    for i in res:
        print(long_to_bytes(i))

#level2
e,g,p=(2685568775701283525351462610033561666387306287538522499134808519515971408889570947875407095838440735098786110848850070468375238474921045086123009358906,
       2,
       3108147961599785276150798080269087679501293709501455568774725039866085754219397531303169017523045103124751042601841840328290404343235853405579539233773)
a,b=(1968486588460454870108621075441203470309302694739442500606039058477890260262954690597523764122825500774397066089804125306327432806567312924827814647950,
     1024812622664084668424411594448713407303536660751692688061972897584163822765150299422248209733371319297760175591974882337903320853550670045641950256872)
       
for i in range(2**16):
    if(pow(g,i,p)==e):
        print(long_to_bytes(i))
        d=i
inv=get_inverse(a,p)
m2=(b*pow(inv,d,p))%p
print(long_to_bytes(m2))

#level3
cipher=[[414,131,27744],
        [249,291,27612],
        [26,255,26656],
        [452,278,31968],
        [78,308,17034],
        [319,33,15400],
        [598,457,51200],
        [310,478,2695],
        [307,739,5500],
        [397,455,89500]
        ]
p=769
a=23
b=711

key=100
k=100
for ci in cipher:
    kG=[0,0]
    kG[0],kG[1]=get_ng(ci[0], ci[1] , k, a, p) 
    decrypto_text_x,decrypto_text_y = get_ng(kG[0], kG[1] , key, a, p)
    print(chr(ci[2]//decrypto_text_x),end="")

tiny_PRNG1：

出题人：DJ

主要是对xoroshiro128plus随机数发生器，参考资料

需要对next函数进行逆向，然后用z3求解种子。

直接放解题脚本：

#!/usr/bin/env python3
# -*- coding: utf-8 -*-
import sys, z3
from sys import argv
from typing import List
from pwn import (
    process,
    remote,
    log,
    # context
)
from Crypto.Util.number import long_to_bytes
# context.log_level = "DEBUG"
bit64 = 0xffffffffffffffff

def LShL(x, n): return (x << n) & bit64

def xo128(x, y, LShR = lambda x,i: x>>i):
    y ^= x
    return y ^ LShL(y, 14) ^ (LShL(x,55)|LShR(x,9)), (LShL(y,36)|LShR(y,28))

def get_output(io, size):
    output = []
    with tqdm(total=size) as bar:
        while len(output) < size:
            io.sendlineafter("> ", "1")
            line = io.recvline().decode("utf-8")
            output += list(map(int, line.strip().split(" ")))
            bar.update(10)
    bar.close()
    return output

def main():
    if len(argv) == 1:
        io = process("./a.out")
    else:
        io = remote(argv[1], int(argv[2]))
    log.info("get output")
    out = get_output(io, 10)
    x0, y0 = z3.BitVecs('x0 y0', 64)
    x, y = x0, y0
    s = z3.SimpleSolver()
    
    for v in out:
        s.add((x + y) & bit64 == v)
        x, y = xo128(x, y, z3.LShR)
    
    ans = []

    for i in range(1, sys.maxsize):
        if s.check().r != 1: break  # quit if failed
        soln = s.model()
        x, y = (soln[i].as_long() for i in (x0,y0))
        ans += ["ACTF{" 
            + long_to_bytes(x).decode("utf-8")[::-1]
            + long_to_bytes(y).decode("utf-8")[::-1]
            + "}"]
        for j in range(10):
            x, y = xo128(x, y)
        s.add( z3.Or(x0 != soln[x0], y0 != soln[y0]) )
    
    for a in ans:
        log.info("possible flag: " + a)

if __name__ == "__main__":
    main()

• 作者： 痛并快乐着
• 文章链接: https://life-extension.github.io/2020/06/05/ACTF2020密码学部分writeup/
• 版权声明: 本博客所有文章除特别声明外,均采用 CC BY-NC-ND 4.0 许可协议。转载请注明出处!

Related post

Comment

Share

To Top «Pre post Next post»

• 通过python脚本自动插入汇编反调试代码

  五月 20日, 2020

  研究背景在之前OLLVM项目的研究过程中，我们发现反调试技术对反混淆脚本有一定的干扰作用，如果可以在OLLVM的中间代码中自动化插入反调试代码，那么就可以给OLLVM的代码混淆增加一层保障。 方案分析探讨多种方案以后，我认为最适合在汇...

  
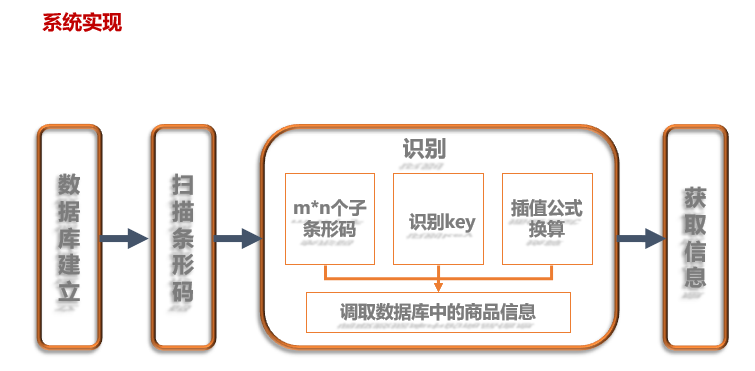
• 基于门限方案的条形码保密及容错技术

  四月 30日, 2020

  关键词：门限方案，条形码保密，条形码容错，条形码认证与防伪造。 经历过初期两个小项目的探索，我们项目团队积累了一定的项目研究经验，在老师和16级学长的帮助下，我们把研究方向转到了门限方案的实际应用上。结合市面上用9张合并的条形码提高条...

  
• 2020新年原创脚本-其中的小把戏你清楚吗

  四月 26日, 2020

  关键词：随机数素数生成，新年祝福小程序。 脚本创作这是我在大年三十写的一个程序，当时我正准备去伯克利交流，但由于疫情的缘故，出国变数增大，所以我就打算通过随机数“未卜先知”。以下就是我的脚本： 12345678910111213141...

  
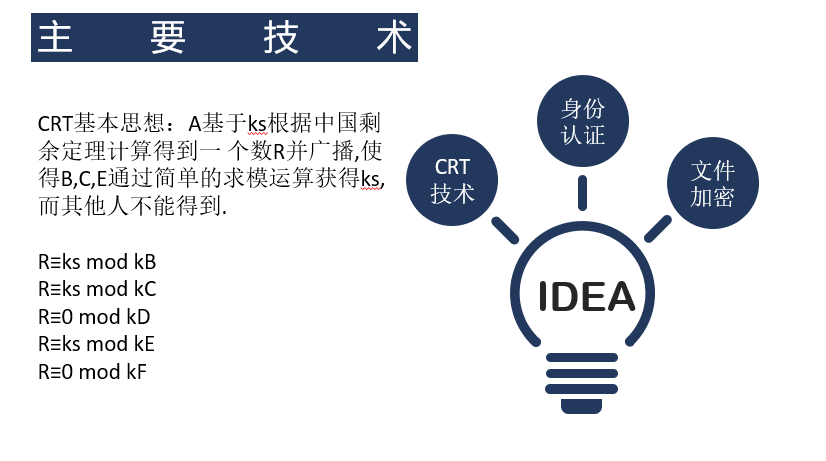
• 基于CRT的物流信息安全处理方案

  四月 15日, 2020

  关键词：中国剩余定理，密钥分发技术，隐私保护。 引言在2018年11月份的时候，段老师在密码学课上讲到了密钥分发协议，我当时就觉得这个协议很有意思也很有应用前景。后来老师还很主动地分享了一下它的idea，其中一部分就是有关物流单上的信...

  
• 基于CRT的新型群文件共享系统

  四月 13日, 2020

  关键词：隐私保护，权限管理，身份认证，中国剩余定理，密钥分发，密钥更新。 这个项目的是在2019年寒假期间进行的，4月份在中南大学信息安全作品赛答辩，但是由于功能只实现了主体部分，加之我在台上比较胆怯紧张，所以只获得团队三等奖，但是当...

  
• 安卓反混淆软件探索-deobf

  三月 19日, 2020

  关键词：代码混淆，代码反混淆及其原理，代码反混淆软件测试与性能对比。 前言我们的大创项目其实是分两方面进行的，一方面，我们从代码混淆的角度比较各种软件对安卓程序的加固能力；另一方面，我们着重针对OLLVM进行反混淆测试。OLLVM集成...

  
• 记一次安卓代码加固软件的测试过程

  三月 13日, 2020

  关键词：代码加固，软件测试，原理分析，过程分析。 在大创项目的实践中，我们对市面上的一些安卓代码加固软件进行了采集，经过搜集，发现了几类代码加固方法并分组进行研究。我发现很多代码加固软件都是对java字节码进行混淆与加固，另外一些则选...

  
• 对OLLVM代码加固技术的改进

  三月 8日, 2020

  1．反静态调试反静态调试可以通过花指令，代码加密，代码加壳等方式实现。 请看图1所示的一段反调试代码： ​ 图1 花指...

  
• OLLVM代码加固机制分析

  二月 24日, 2020

  我们通过自己编写测试代码，再用OLLVM的不同指令进行加固，并逆向查看加固效果，加深对代码加固机理的了解。OLLVM目前提供的功能包括控制流平坦化（fla指令），指令替代（sub指令），代码虚拟化（bcf指令）以及虚假控制流（obf指...

  
• 对音频缓存加密的探讨

  二月 17日, 2020

  关键词：缓存解密，批量自动执行脚本，版权保护相关建议。 前段时间，某音乐被爆其缓存文件只使用了简单的异或加密，且容易得到加密密钥为0xa3。原文链接点击这里。以下是我的延伸探讨。 1.对音频缓存的批量解密攻击抱着好奇的心理，我把手机...

  

Please check the parameter of comment in config.yml of hexo-theme-Annie!